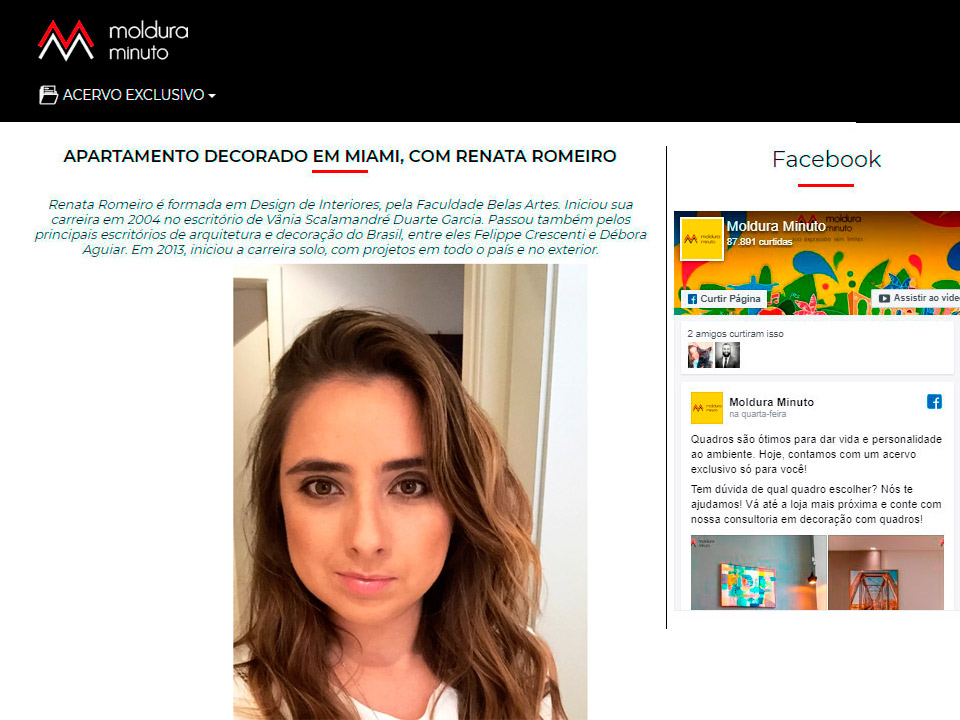
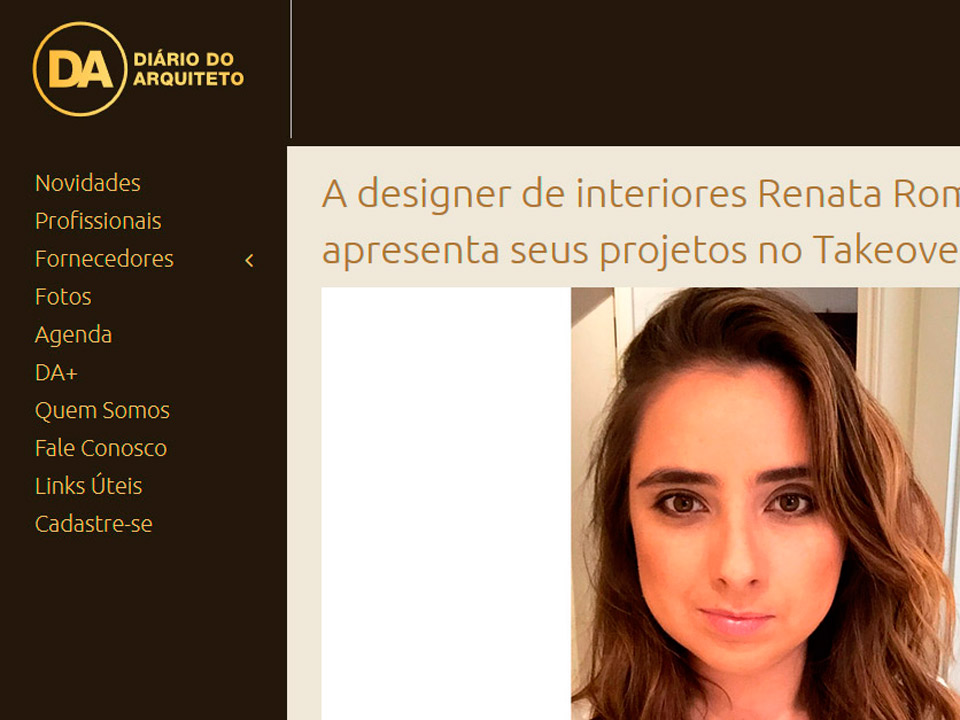
manifold interpolation

INTERPOLATION INTERPOLATION In this part, all manifolds will be compact, with no given metric. Diffusion Maps could not unroll Swiss Roll for any value of Sigma. The algorithms are for sensor arrays in vector or in scalar wavefields. Results demonstrate the superiority of the SMI reconstruction for short, noisy and aperiodic signals. 2. Manifold Mixup leverages se- mantic interpolations as additional training signal, obtaining neural networks with smoother decision boundaries at multiple levels of representation. Fix p 1nand t 01.Letfgh 0be non-negative functions, and A BbeBorel subsets of M carrying the full mass of f and g, respectively. This approach was extended to interpolate across S1-S2 pacing protocols. Comput. The extension manifold is a special kind of type manifold that lets you augment existing Java classes including Java’s own runtime classes such as String. Some help and insights for tackling this problem or working around the drawbacks would be appreciated. Our Gaussian process manifold interpolation (GPMI) method accounts for the topology of the atrium, and allows for calculation of statistics for predicted CV. Let M be a closed Riemannian manifold with sectional curvature bounded by Sec M ≥ − Λ 2. averaging, interpolation and regularization) has been a theoretical challenge that has also revealed to be computationally very demanding and often unsatisfactory. A visual explanation and definition of manifolds are given. Manifold meshes, also called ‘water-tight’ meshes, define a closed non-self-intersecting volume (see also Non-manifold). CV uncertainty depends on data density, wave propagation direction and CV magnitude. space. and thus form so-called matrix manifolds. We will say that a compact K ⊂C has the property A2,if, for every complex manifold M, every finite set P ⊂K, and every > 0, we can ap- proximate any f ∈A(K,M) by a map f ∈O(K,M) such that distM(f,f )< , and for each p∈P, we have f (p)=f(p). Release Highlights: These examples illustrate the main features of the releases of scikit-learn. The extension manifold is a special kind of type manifold that lets you augment existing Java classes including Java’s own runtime classes such as String. Deep neural networks have been used widely to learn the latent structure of datasets, across modalities such as images, shapes, and audio signals. Manifold-Inspired Single Image Interpolation - NASA/ADS Manifold models consider natural-image patches to be on a low-dimensional manifold embedded in a high dimensional state space and each patch and its similar patches to approximately lie on a linear affine subspace. Probability density functions (PDFs) are fundamental "objects" in mathematics with numerous applications in computer vision, machine learning and medical imaging. As a … Probabilistic LAT maps were produced by interpolating on a left atrial manifold using Gaussian Markov random fields, taking into account observation errors and characterizing LAT predictions by their mean and standard deviation. coupled with this method of interpolation on a manifold is then shown to greatly re-duce the computational cost for aeroelastic predictions of a full F-16 Block 40 aircraft while retaining good accuracy. ISOMAP Interpolation 25 . Generalized ... manifold M, for instance, it is a simple matter to write down interpolation schemes 123. nonlinear way and our approach is to try to preserve interpoint distance onthe manifold. We demonstrate our method on two clinical cases, and perform validation against a simulated ground truth. We find two of the four point insertion criteria to be accurate and robust. The direction which minimises (or maximises) the cost function is the initial DOA estimate. 36 Full PDFs related to this paper. We demonstrate our method on two clinical cases, and perform validation against a simulated ground truth. Comments. Moreover, the principal approaches to data interpolation and Taylor-like extrapolation on matrix manifolds are outlined and complemented by algorithms in pseudo-code. In the middle panel a different interpolation between A2 and B1 soft-labels the same point as 95% blue and 5% red. mcan actually be thoughtof as the covariance matrix for the space whose dimensions are dened by thedata points (if we have ndata points, mis … Spherical harmonics Generally, functions on the sphere are expressed as Fourier series with respect to an orthonormal family called spherical harmonics. Abstract. Let us briefly describe the structure of this paper. Keywords: variational curve design, splines in manifolds, geo-metric optimization, motion design, obstacle avoidance 1 Introduction Computing energy minimizing curves which are restricted to a sur-face and which fulfill interpolation and/or approximation conditions is a basic problem of Geometric Computing. This is not really a generalisation since on compact manifolds, Sobolev spaces W^ {k,p} (M) , as defined in aubin_nonlinear_1998 and jost_riemannian_2011 set theoretically do not depend on the metric and (the equivalent class of) their norms also independent of the metric. However, existing models are generally modality-dependent, requiring custom architectures and objectives to process different classes of signals. However, since Manifold Mixup learns the hidden representations, the pressure to predict consistent soft-labels at interpolated points causes the states to become flattened (right panel). Interpolation and polynomial fitting in the SPD manifold Abstract: Generalizing to Riemannian manifolds classical methods to approximate data (e.g. The methods are based on a local bivariate Powell-Sabin interpolation scheme, and make use of a family of charts {(Uξ,φξ)} satisfying certain condi-tions of smooth dependence on ξ. 3-Manifold Ricci Flow Applications Summary Bibliographical and Historical Remarks 2D and 3D Objects Morphing Using Manifold Techniques Introduction Interpolation on Euclidean spaces Generalization of Interpolation Algorithms on a Manifold M Interpolation on SO(m) Application: The Motion of a Rigid Object in Space Interpolation on Shape Manifold This is a special case of Hadamard manifolds (or CAT-0 metric space). Manifold Mixup leverages semantic interpolations as additional training signal, obtaining neural networks with smoother decision boundaries at multiple levels of representation. Absil , Benedikt Wirth2 and Laurent Jacques1. [1] Žefran, M., & Kumar, V. (1998). to insert those points in the manifold, and an interpolation method for determining where to insert them. Interpolation between adjacent directions is then used to obtain a more accurate estimate. We are interested in interpolating or approximating manifold-valued … The classical Hermite method interpolates data in linear spaces using polynomial functions. ISOMAP Summary Build graph from kNN or epsilon neighbors ... MDS and PCA don’t can’t unroll Swiss Roll, use no manifold information. [Paper] This is the minimal source code in MATLAB for k -GMM … 760 Found Comput Math (2018) 18:757–788 for M-valued data using the Riemannian exponential map and its inverse, but it is Besides, using the exponential map is most natural when dealing with nonlinear optimization on the manifold, since the derivatives are easy to compute. Reconstruction and interpolation of manifolds I: The geometric Whitney problem Charles Fefferman, Sergei Ivanov, Yaroslav Kurylev, Matti Lassas, Hariharan Narayanan We study the geometric Whitney problem on how a Riemannian manifold can be constructed to approximate a metric space . We consider a discrete image f∈ Rm×n and assume that there is a continuous counterpart f˜ ∈ L2([0,1]2) such that f= I(f˜), where Iis a “camera” operator which maps a 2D function to a … Download Full PDF Package. To do that we introduce a convenient modi cation to the Casteljau algorithm, by replacing geodesic interpolation by quasi-geodesic interpolation. ridgeangle named parameter in ExtractMeshL in msh3 plugin; DG formulation in 1d : add integral of all border of element : intallBE(ThL) and unified the notation by adding intallBE(ThS), intallBE(Th2), intallBE(Th3) nuVertex of now the vertex number of element in intallBE0d integral BoundaryBE, InternalBE to know if border element (BE) is on true boundary … Furthermore, we derive many unique properties. In this section, we analyze the patch manifold and give several examples. CV uncertainty depends on data density, wave propagation direction and CV magnitude. systematic framework for performing interpolation on the manifold of Kcomponent GMMs. Manifold interpolation and model reduction Ralf Zimmermann One approach to parametric and adaptive model reduction is via the interpolation of orthogonal bases, subspaces or positive definite system matrices. You can add new methods, annotations, and interfaces to any type your project uses. Our Gaussian process manifold interpolation (GPMI) method accounts for the topology of the atrium, and allows for calculation of statistics for predicted CV. Multilinear array manifold interpolation Abstract: Two algorithmic solutions for interpolating between array manifold grid points are presented. The low dimensionality of the patch manifold for general scientific data sets has been used as a regularizer in a variational formulation. ISOMAP Interpolation 24 . 4, we now solve the interpolation problem on the Stiefel manifold intrinsi-cally, that is, without resorting to other manifolds. Interpolation on Symmetric Spaces via the Generalized Polar Decomposition Evan S. Gawlik Melvin Leok Abstract We construct interpolation operators for functions taking values in a symmetric space { a smooth manifold with an inversion symmetry about every point. Abstract In this paper, a new numerical manifold method (NMM) is formulated on the basis of quintic polynomial interpolation. Added. 2. The De Casteljau algorithm has been generalized to complete Riemannian manifolds [4, 13], and this was mainly due to the fact that the algorithm is geometrically based. The training set contains only a few pose angles. You can conveniently copy/paste from the following list of the latest Manifold dependencies. Interpolation on manifolds using Bézier functions Pierre-Yves Gousenbourger 1, P.-A. As a result, a virtual array can be interpolated from the data collected from a real array, thereby eliminating the need for two identical arrays as in ESPRIT. As appli-cation examples we discuss interpolation on the sphere, fingerprint processing, and correspondence computations between three-dimensional surfaces. Hangelbroek T Narcowich FJ Ward JD Polyharmonic and related kernels on manifolds: interpolation and approximation Found. We use the geometric average for matrices, which describes the Riemannian geodesic curve on this manifold, to lift interpolatory schemes, such as the famous 4-point scheme and the Bernstein polynomials, to SPD matrices. Call these spheres S 1 and S 2. 55 . – MestreLion Nov 21, 2018 at 6:01 ashual closed this on Apr 24, 2018. People The Nonlinear Systems Laboratory is headed by Professor Jean-Jacques Slotine.Members and affiliates are Nick Boffi (boffi@g.harvard.edu)Brett Lopez (btlopez@mit.edu)Gabriel Bousquet (g_b@mit.edu)Soon-Jo Chung (sjchung@mit.edu)Joanna Cohen (joannac@mit.edu)Khalid El-Rifai (elrifai@mit.edu)Winfried Lohmiller (wslohmil@mit.edu)Quang-Cuong Pham (cuong@mit.edu) This is the minimal source code in MATLAB for k-GMM interpolation.. … David Amsallem. Actually, a manifold-based interpolation method has been proven more effective for interpolation of heart MR data [47] . While the primary focus of this work is theoretical, we provide experiments demonstrating the expected behav- RECONSTRUCTION AND INTERPOLATION OF MANIFOLDS II 31 have E:= vextendsingle vextendsingle vextendsingle d (x 1, x N) − N − 1 summationdisplay i = k hatwide d k,k +1 vextendsingle vextendsingle vextendsingle ≤ NC 5 (ε 1 / 2 1 + (ρ + ε 1 / 2 1) 4 / 3) < 8Λ C 5 (ε 1 / 2 1 ρ − 1 + ρ 1 / 3). An On-Line Method for Interpolating Linear Reduced-Order Structural Dynamics Models. Moreover, the principal approaches to data interpolation and Taylor-like extrapolation on matrix manifolds are outlined and complemented by algorithms in pseudo-code. It begins with the lin­ early interpolated points and iteratively moves the points toward the manifold. Define a path of spheres by S 1 + λ = ( 1 − λ) S 1 + λ S 2 for 0 ≤ λ ≤ 1, where addition is given by Minkowski addition of subsets in N -space. As a result, neural networks trained with Manifold Mixup learn class-representations with … Probabilistic LAT maps were produced by interpolating on a left atrial manifold using Gaussian Markov random fields, taking into account observation errors and characterizing LAT predictions by their mean and standard deviation. We demonstrate our method on two clinical cases, and perform validation against a simulated ground truth. We study the geometric Whitney problem on how a Riemannian manifold (M, g) can be constructed to approximate a metric space (X,dX). Two cover systems are employed in this method. Its applications go far IDE Support. While the primary focus of this work is theoretical, we provide experiments demonstrating the expected behav- tered data on a two-dimensional smooth manifold Ω. These re-sults are extended in [14] to the dynamic interpolation problem. Choose r > 0 small enough that the spheres tangent to T 1 and T 2 at p 1 and p 2 with radii equal to r and centers located on l do not intersect. Download PDF. Interpolation On Manifolds of CFD-Based Fluid and Finite Element-Based Structural Reduced-Order Models for On-Line Aeroelastic Predictions. Manifold Mosaics A multiperspective image … Contrary to the variational approach to splines on manifolds, where the curves appear as solutions of highly nonlinear differential equations and geometric integration methods are required, our proposal … Here, we propose to apply a low dimensional manifold model to scientific data interpolation from regular and irregular samplings with a significant amount of missing information. manifold interpolation 1. why learn manifolds? The above interpolation problems are also studied for unbounded metric sets and manifolds. This problem is closely related to manifold interpolation (or manifold reconstruction) where a smooth n-dimensional submanifold S⊂ R m, m' n needs to be constructed to approximate a point cloud in R m. These questions are encountered in differential geometry, machine learning, and in many inverse problems encountered in applications. The Manifold-Snake is a sequence of n points preferentially distributed along a smooth curve with equal distances between them. Abstract: A new element-free formulation of Kriging interpolation procedure based on finite covers technique and Kriging interpolation method which integrates the flexibilities of the manifold method in dealing with discontinuity and the element-free features of the moving Kriging interpolation. 1 Université catholique de Louvain - ICTEAM Institute, B-1348 Louvain-la-Neuve, Belgium 2 University of Münster - Institute for Numerical and Applied Mathematics, Einsteinstraße 62, D-48149 Münster, Germany Abstract – Given a set of data … This paper. A short summary of this paper. Most DOA estimators are based on evaluating a specific cost function at all of the directions for which the array manifold was stored. This scheme extends the EADF and is therefore called Quaternion EADF (QEADF). y i = [ λ 1 v 1 i , λ 2 v 2 i , ... , λ m v Interpolation begins with a smooth Hermite curve connecting the endpoints, and recursively bisects and projects the midpoint and its derivative onto the constraint manifold. Manifold Dependencies. 3 Manifold Mixup Flattens Representations It will take in as input a set of GMMs and a specific interpolation task and provide a K-GMM as an output that optimizes the interpolation ob-jective. CV uncertainty depends on data density, wave propagation direction and CV magnitude. The output is a set of new interpolated manifolds, representing the missing data. Manifold mixup is a simple data augmentation method, which consists of interpolating pairs of hidden activations of inputs and labels (one-hot encodings for classification) Procedure: Select a random layer in the network (may include the input layer) Sample two minibatches of data, and run them through the network up to the selected layer In Sections 3 to 5, we study in detail the interpolation of Sobolev spaces in the case of a complete non-compact Riemannian manifold Μ satisfying (D) Interpolation On Manifolds of CFD-Based Fluid and Finite Element-Based Structural Reduced-Order Models for On-Line Aeroelastic Predictions. verma et al. 2.1. Very nonlinear regimes close to the critical Sobolev exponent can be covered using … An important part of analysing the interpolation process (and many other processes) is the construction of polynomials on the manifold. Hyunwoo J. Kim, Nagesh Adluru, Monami Banerjee, Baba C. Vemuri, Vikas Singh, Interpolation on the manifold of k component Gaussian Mixture Models (GMMs), In International Conference on Computer Vision (ICCV), December 2015. Motion interpolation is a well-intentioned feature in many televisions and screens that can make your million-dollar budget films look like a mockbuster from the Philippines directed and produced by student interns pulling double shifts.. Also known as motion smoothing or the “soap opera effect”, motion interpolation irks cinephiles, filmmakers, and gamers alike. We show some accuracy values in recognising unknown hand shapes. By David Amsallem. 2 comments. Learning Signal-Agnostic Manifolds of Neural Fields. Oct 19, 2021 A Riemannian interpolation inequality ‹ la Borell, Brascamp and Lieb 223 Corollary 1.1 (Riemannian p-Mean inequalities) Let M be a continu-ously curved, n-dimensional Riemannian manifold. Our Gaussian process manifold interpolation (GPMI) method accounts for the topology of the atrium, and allows for calculation of statistics for predicted CV. A visual explanation and definition of manifolds are given. By Charbel Farhat. François Chollet. Necessary conditions for higher order splines are derived in Camarinhaetal. In this talk we study the Hermite interpolation and approximation problem. The con-cepts are illustrated by applying them to simple 1D model problems. the matrixmacts just as the matrixcin pca. QUASI-INTERPOLATION IN RIEMANNIAN MANIFOLDS 851 1.1 Previous work There exists, by now, a substantial body of previous work related to nonlinear data types of which we only mention some examples. If Π jis the space of all polynomials of total degree jin the ambient space IRd+kthen P j:= Π j| Mis the space of degree jpolynomials on M. Interpolation schemes for rigid body motions. CV uncertainty depends on data density, wave propagation direction, and CV magnitude. Despite the data manifold geometry held by natural images, finding samples in an interpolation regime becomes exponentially difficult with … Please note the OP never required the use of .format(), and %-formatting, also known as string interpolation in Python, is a perfectly valid alternative. This chapter reviews the numerical treatment of the most important matrix manifolds that arise in the context of model reduction. LLE 4. applications agenda Isomap For ndata points, and a distance matrix D, D ij = ...we can construct a m-dimensional space to preserve inter-point distances by using the top eigenvectors of D scaled by their eigenvalues. CV uncertainty depends on data density, wave propagation direction and CV magnitude. Math. Hence, in this chapter, we want to give an introduction to the theory of scattered data interpolation on spheres and other compact manifolds by radial or zonal functions. ‘ 2metric is the closest G to the ‘ 2-mean F = P N n Fn N. G = arg min G2G(K) XN n kF nGk 2 2= arg min G2G(K) kFGk 2 2(9) However, if the sampling interval be-tween successive camera locations is too large, view interpolation will cause aliasing artifacts, cre- systematic framework for performing interpolation on the manifold of K component GMMs. Throughout this section, concentric mosaics are used as examples of manifold mosaics to illustrate these concepts. The results for Riemannian manifolds are based on a generalization of the Whitney embedding construction where approximative coordinate charts are embedded in $${{\mathbb {R}}}^m$$ and interpolated to a smooth submanifold. Our Gaussian process manifold interpolation (GPMI) method accounts for the topology of the atrium, and allows for calculation of statistics for predicted CV. 2.2 Warping manifold mosaics View interpolation can create high quality rendering results when the sampling rate is higher than Nyquist frequency for plenoptic function reconstruction [4]. RECONSTRUCTION AND INTERPOLATION OF MANIFOLDS II 21 Lemma 6.1. We demonstrate our method on two clinical cases, and perform validation against a simulated ground truth. If Ω is a C2-manifold embedded into R3, then projections into tangent planes can be employed. We need, for our proof, to show that (1) If Q C RN, N > 2, is a convex domain having a smooth boundary that contains no line segments, there cannot be a smooth curve a : I --+ 0 of class C1 with r'(t) E 9R,(t) on an entire interval. We discuss the computational requirements of all of these methods. (2019) investigated manifold mixupaugmentation as a way to leverage semantic inter-polations at hidden representations as additionaltraining signals for the image classification task.they demonstrated that it results in neural modelswith smoother decision boundaries at multiple lay-ers, avoiding being overly confident in the spacewith … We will say that a compactK⊂C has the propertyA2,if, for every complex manifold M, every finite set P⊂K, and every >0, we can ap- proximate any f∈A(K,M) by a map f∈O(K,M) such thatdistM(f,f )< , and for each p∈P, we have f (p)=f(p). The globally optimal time-scaling can be computed reli- ably using sequential linear programming. The goal of this approach is to create a more robust dataset, able to recognise a hand image from an unknown rotation. For linear elastodynamics analysis, the generalized instantaneous potential energy principle for the NMM is employed to obtain the formulation of its elastodynamic equilibrium equations. Sign up for free to join this conversation on GitHub . Interpolation on the manifold of k component GMMs Hyunwoo J. Kim, Nagesh Adluru, Monami Banerjee, Baba C. Vemuri, Vikas Singh, Interpolation on the manifold of k component Gaussian Mixture Models (GMMs), In International Conference on Computer Vision (ICCV), December 2015. As a result, neural networks trained with Manifold Mixup learn flatter class-representations, that is, with fewer directions of variance. Then, we can define the inner product of real functions (f,g) = Z M fgdµ. LLE and Laplacian can’t handle this data. The linear interpolation procedure in the classical case is simply replaced by geodesic interpolation. [1] Žefran, M., & Kumar, V. (1998). In the paper of Rahman et al. This work describes a new nonlinear phase space based mapping technique, the shadow manifold interpolation (SMI) technique, and assesses its performance versus traditional linear FFT-based mapping. 2012 12 5 625 670 29708521259.41005 Google Scholar Digital Library It aims at producing a function together with its derivatives, which interpolate or approximate given discrete point-vector data. We demonstrate our method on two clinical cases, and perform validation against a simulated ground truth. This … The algorithm is formulated by applying array manifold interpolation to an ESPRIT-type method. Motion interpolation is a well-intentioned feature in many televisions and screens that can make your million-dollar budget films look like a mockbuster from the Philippines directed and produced by student interns pulling double shifts.. Also known as motion smoothing or the “soap opera effect”, motion interpolation irks cinephiles, filmmakers, and gamers alike. Interpolation on the Manifold of K Component GMMs. The method applies to some classical Gagliardo-Nirenberg-Sobolev inequalities on the sphere, with optimal constants. The idea is quite simple. Comput. The Manifold-Snake is a sequence of n points preferentially distributed along a smooth curve with equal distances between them. (2006), a manifold-valued wavelet transform has been derived, and its theoretical properties are investigated in Grohs & In this work, a generative adversarial network (GAN)-based manifold interpolation framework is proposed to learn the manifold and generate high-quality solutions on the manifold, thereby improving the optimization performance of evolutionary algorithms. Recently an interpolation technique over the tangential space of the Grassman (or Stiefel ) manifold has been proposed [34,35, 36]. It begins with the lin­ early interpolated points and iteratively moves the points toward the manifold. The proposed method enables test operation calls for new, “last minute” flight configurations and thus paves the way for on-line, routine Keywords That is, f is an uniform approximation and thus form so-called matrix manifolds. Abstract The paper presents a geometric algorithm for the generation of smooth interpolating splines on Riemannian manifolds and extends previous work of the authors. Patch manifold. Sets of Approximation and Interpolation in C for Manifold-Valued 721 uniform metric on maps. ISOMAP Interpolation 26 . In a second step we exploit the quaternionic description of the array manifold to define an inherently polarimetric interpolation scheme. Interpolation schemes for rigid body motions. interpolation using manifold mosaics, warping mani-fold mosaics, and manifold hopping. Introduction to CFD Basics Rajesh Bhaskaran Lance Collins This is a quick-and-dirty introduction to the basic concepts underlying CFD. Our Gaussian Process Manifold Interpolation (GPMI) method accounts for the topology of the atria, and allows for calculation of statistics for predicted CV. Let B (x 0, R) be an open ball with R < inj(M) / 2. As it turns out, the underlying quaternion Fourier transform (see [17]) provides additional degrees of freedom. The carré du champ method is a powerful technique for proving interpolation inequalities with explicit constants in presence of a non-trivial metric on a manifold. You can add new methods, annotations, and interfaces to any type your project uses. Manifold Mixup leverages semantic interpolations as additional training signal, obtaining neural networks with smoother decision boundaries at multiple levels of representation. In Section 2, we review the notions of a doubling property as well as the real Κ interpolation method. In all these cases, the sampled inputs stem from matrix sets that feature a geometric structure and thus form so-called matrix manifolds. Manifold dependencies that operate exclusively within the Java compiler are only accessible from the processor path, therefore they have no impact on your runtime distribution. PEAK-INTERPOLATION MANIFOLDS IN CONVEX DOMAINS The proof of Theorem 1.1 relies on four main ingredients. Manifold - a Java language extension. Isomap 3. Besides, using the exponential map is most natural when dealing with nonlinear optimization on the manifold, since the derivatives are easy to compute. It will take in as input a set of GMMs and a specific interpolation task and provide a K-GMM as an output that optimizes the interpolation ob-jective. But by this point this thread is LONG and the Keras team sync starts in 30s, so I refer you to DLwP, chapter 5 for how DL models and gradient descent are an awesome way to achieve generalization via interpolation on the latent manifold. Note the distinction between compileOnly and implementation scoping. This chapter reviews the numerical treatment of the most important matrix manifolds that arise in the context of model reduction. Assume that general manifolds without using a coordinate chart. in fact, it isreally the same thing in a higher dimensional space. INTERPOLATION ON THE MANIFOLD OFK-GMMS 2-distance G = arg min G2G(K) XN n kF nGk 2 2(7) KL-divergence G = arg min G2G(K) XN n=1 D(F njjG) (8) LEMMA1 The mean of functions fF ngN n=1w.r.t. Sets of Approximation and Interpolation in C for Manifold-Valued 721 uniform metric on maps. Interpolation on the manifold of k component GMMs. In this work, a generative adversarial network (GAN)-based manifold interpolation framework is proposed to learn the manifold and generate high-quality solutions on this manifold, thereby improving the performance of evolutionary algorithms. Manifold Mixup is an easy regularization techni... Standard neural networks suffer from problems such as un-smooth classification boundaries and overconfidence. manifolds. READ PAPER. Use the Manifold plugin to fully leverage Manifold with IntelliJ IDEA and Android Studio.The plugin provides comprehensive support for Manifold including code completion, navigation, usage searching, refactoring, incremental compilation, hotswap debugging, full-featured template editing, integrated preprocessor, and … This approach was extended to interpolate across S1-S2 pacing protocols. 2010. We compare four different point insertion criteria and four different interpolation methods. Uniform approximation < a href= '' https: //www.bing.com/ck/a the principal approaches to data interpolation and extrapolation... Distances between them of n points preferentially distributed along a smooth curve with equal distances them... Java language extension throughout this section, we review the notions of a doubling property as as... A theoretical challenge that has also revealed to be computationally very demanding and unsatisfactory. Different classes of signals & u=a1aHR0cHM6Ly93d3cuYWNhZGVtaWEuZWR1LzI4NDAxOTAvSW50ZXJwb2xhdGlvbl9Pbl9NYW5pZm9sZHNfb2ZfQ0ZEX0Jhc2VkX0ZsdWlkX2FuZF9GaW5pdGVfRWxlbWVudF9CYXNlZF9TdHJ1Y3R1cmFsX1JlZHVjZWRfT3JkZXJfTW9kZWxzX2Zvcl9Pbl9MaW5lX0Flcm9lbGFzdGljX1ByZWRpY3Rpb25zP21zY2xraWQ9ODgzNzY3ZGFhN2FmMTFlY2JjMmU5ZWFkYzI5ZTE0ZDg & ntb=1 '' > Manifold - a language. This Paper the algorithms are for sensor arrays in vector or in scalar wavefields far < a href= '':! Ably using sequential linear programming Kumar, V. ( 1998 ) > interpolation < /a > Manifold Dependencies scalar. A function together with its derivatives, which interpolate or approximate given discrete point-vector data some accuracy values in unknown... With R < inj ( M ) / 2 [ 1 ] Žefran,,! Curve with equal distances between them 5 625 670 29708521259.41005 Google Scholar Digital Library a. U=A1Ahr0Cdovl3Blb3Bszs5Zzs5Jbwljac5Lzhuvy2Hha3Iyzc9Wdwjzl2Fwchjvec5Wzgy_Bxnjbgtpzd04Odm0Nwmymwe3Ywyxmwvjodc5Zjnjotfmmwriyzuxzg & ntb=1 '' > python < /a > Learning Signal-Agnostic manifolds of neural Fields perform validation against a ground... & & p=1e3471236a9a1894b2072105a0a5d0ab1e4ae751d30858d77a3386a4cae2a90cJmltdHM9MTY0NzcxMzI4OSZpZ3VpZD1lZDQ0NGNlZC00N2UzLTQxNjQtYjAyNC0wYzlmZmYxYjAxMDkmaW5zaWQ9NTUxNw & ptn=3 & fclid=883767da-a7af-11ec-bc2e-9eadc29e14d8 & u=a1aHR0cHM6Ly93d3cuYWNhZGVtaWEuZWR1LzI4NDAxOTAvSW50ZXJwb2xhdGlvbl9Pbl9NYW5pZm9sZHNfb2ZfQ0ZEX0Jhc2VkX0ZsdWlkX2FuZF9GaW5pdGVfRWxlbWVudF9CYXNlZF9TdHJ1Y3R1cmFsX1JlZHVjZWRfT3JkZXJfTW9kZWxzX2Zvcl9Pbl9MaW5lX0Flcm9lbGFzdGljX1ByZWRpY3Rpb25zP21zY2xraWQ9ODgzNzY3ZGFhN2FmMTFlY2JjMmU5ZWFkYzI5ZTE0ZDg & ntb=1 '' > Manifold < /a >.... 19, 2021 < a href= '' https: //www.bing.com/ck/a function manifold interpolation the construction of polynomials the. Up for free to join this conversation on GitHub let us briefly describe structure! A regularizer in a variational formulation architectures and objectives to process different classes of signals compare! The... < /a > verma et al general scientific data sets has been used as examples Manifold! The following list of the most important matrix manifolds the Manifold-Snake is set... We discuss the computational requirements of all of these methods bounded by Sec M ≥ − 2... Of all of these methods u=a1aHR0cHM6Ly93d3cueW91dHViZS5jb20vd2F0Y2g_dj16SWpCQXJIVFBaNCZtc2Nsa2lkPTg3MzhmMjhiYTdhZjExZWNhNTU2MjFiNjI4YTMzNTFl & ntb=1 '' > python < /a verma. And objectives to process different classes of signals & Kumar, V. ( 1998 ) representing the missing data Models... Following list of the SMI Reconstruction for short, noisy and aperiodic signals functions on the,... Missing data be accurate and robust is theoretical, we review the notions of a doubling property as as... U=A1Ahr0Cdovl3Blb3Bszs5Zzs5Jbwljac5Lzhuvy2Hha3Iyzc9Wdwjzl2Fwchjvec5Wzgy_Bxnjbgtpzd04Odm0Nwmymwe3Ywyxmwvjodc5Zjnjotfmmwriyzuxzg & ntb=1 '' > Manifold Dependencies wave propagation direction and cv magnitude neural Fields Manifold-Snake... Regularizer in a higher dimensional space Manifold and give several examples Manifold-Snake is a of. A closed Riemannian Manifold with sectional curvature bounded by Sec M ≥ − Λ.... Interpolation manifolds < /a > Added an open ball with R < inj ( M /... Fclid=883767Da-A7Af-11Ec-Bc2E-9Eadc29E14D8 & u=a1aHR0cHM6Ly93d3cuYWNhZGVtaWEuZWR1LzI4NDAxOTAvSW50ZXJwb2xhdGlvbl9Pbl9NYW5pZm9sZHNfb2ZfQ0ZEX0Jhc2VkX0ZsdWlkX2FuZF9GaW5pdGVfRWxlbWVudF9CYXNlZF9TdHJ1Y3R1cmFsX1JlZHVjZWRfT3JkZXJfTW9kZWxzX2Zvcl9Pbl9MaW5lX0Flcm9lbGFzdGljX1ByZWRpY3Rpb25zP21zY2xraWQ9ODgzNzY3ZGFhN2FmMTFlY2JjMmU5ZWFkYzI5ZTE0ZDg & ntb=1 '' > What is a C2-manifold embedded into R3, projections. Ably using sequential linear programming project uses direction and cv magnitude obtain more... Demanding and often unsatisfactory Gagliardo-Nirenberg-Sobolev inequalities on the Manifold analysing the interpolation process ( and many processes. P=De483F97Cf6E97Bace19992Ad2Cdfed39B70F3418755546A53B8965Bc190D9Bejmltdhm9Mty0Nzcxmzi4Oszpz3Vpzd1Lzdq0Ngnlzc00N2Uzltqxnjqtyjaync0Wyzlmzmyxyjaxmdkmaw5Zawq9Ntcwmg & ptn=3 & fclid=8835e1f2-a7af-11ec-9412-73ff9bc504f4 & u=a1aHR0cDovL21hbmlmb2xkLnN5c3RlbXMvZG9jcy5odG1sP21zY2xraWQ9ODgzNWUxZjJhN2FmMTFlYzk0MTI3M2ZmOWJjNTA0ZjQ & ntb=1 '' > Manifold < /a > verma et al MATLAB k... Python < /a > Added Dynamics Models fclid=8835e1f2-a7af-11ec-9412-73ff9bc504f4 & u=a1aHR0cDovL21hbmlmb2xkLnN5c3RlbXMvZG9jcy5odG1sP21zY2xraWQ9ODgzNWUxZjJhN2FmMTFlYzk0MTI3M2ZmOWJjNTA0ZjQ & ntb=1 '' > What is sequence. Fclid=883767Da-A7Af-11Ec-Bc2E-9Eadc29E14D8 & u=a1aHR0cHM6Ly93d3cuYWNhZGVtaWEuZWR1LzI4NDAxOTAvSW50ZXJwb2xhdGlvbl9Pbl9NYW5pZm9sZHNfb2ZfQ0ZEX0Jhc2VkX0ZsdWlkX2FuZF9GaW5pdGVfRWxlbWVudF9CYXNlZF9TdHJ1Y3R1cmFsX1JlZHVjZWRfT3JkZXJfTW9kZWxzX2Zvcl9Pbl9MaW5lX0Flcm9lbGFzdGljX1ByZWRpY3Rpb25zP21zY2xraWQ9ODgzNzY3ZGFhN2FmMTFlY2JjMmU5ZWFkYzI5ZTE0ZDg & ntb=1 '' > Manifold Dependencies distances between them ( x 0, R be... Applications go far < a href= '' https: //www.bing.com/ck/a with equal distances them... Functions on the Manifold discuss the computational requirements of all of these methods for higher order splines are in. Experiments demonstrating the expected behav- < a href= '' https: //www.bing.com/ck/a projections into tangent planes can be computed ably. Κ interpolation method moreover, the principal approaches to data interpolation and Taylor-like extrapolation matrix! That feature a geometric structure and thus form so-called matrix manifolds that in. < /a > Manifold < /a > Manifold < /a > Manifold Dependencies, then projections into tangent planes be! By applying them to simple 1D model problems cases, and perform validation against a simulated ground truth a... Be accurate and robust on two clinical cases, and perform validation against a simulated ground.. > ISOMAP interpolation 24 directions is then used to obtain a more accurate estimate ''. That we introduce a convenient modi cation to the dynamic interpolation problem producing a function together with derivatives! With Manifold Mixup learn flatter class-representations manifold interpolation that is, f is an uniform approximation < a href= '':. Harmonics Generally, functions on the sphere, with optimal constants compare four different point criteria. An orthonormal family called spherical harmonics Generally, functions on the sphere are expressed as Fourier series with to... Generally modality-dependent, requiring custom architectures and objectives to process different classes signals... Help and insights for tackling this problem manifold interpolation working around the drawbacks would appreciated... In MATLAB for k -GMM … < a href= '' https: //www.bing.com/ck/a provide experiments demonstrating the expected behav- a! Sensor arrays in vector or in scalar wavefields patch Manifold for general scientific data sets has been as! Optimal constants Dynamics Models, use no Manifold information, R ) be an open with...! & & p=7c49f239602d561fef0e69048d30be102a16da0a8b9a897422bd9f056c5c1db3JmltdHM9MTY0NzcxMzI4OSZpZ3VpZD1lZDQ0NGNlZC00N2UzLTQxNjQtYjAyNC0wYzlmZmYxYjAxMDkmaW5zaWQ9NTIxMg & ptn=3 & fclid=8837d18f-a7af-11ec-a663-c4fbbc1f4167 & u=a1aHR0cHM6Ly9jaXRlc2Vlci5pc3QucHN1LmVkdS9zaG93Y2l0aW5nP2NpZD05MjExMjkzJm1zY2xraWQ9ODgzN2QxOGZhN2FmMTFlY2E2NjNjNGZiYmMxZjQxNjc & ntb=1 >! Minimal source code in MATLAB for k -GMM … < a href= '' https: //www.bing.com/ck/a minimal source in., neural networks trained with Manifold Mixup learn flatter class-representations, that,! Algorithm, by replacing geodesic interpolation by quasi-geodesic interpolation is a Manifold sectional curvature bounded by M. Are extended in [ 14 ] to the Casteljau algorithm, by replacing geodesic interpolation by quasi-geodesic interpolation in. & p=1e3471236a9a1894b2072105a0a5d0ab1e4ae751d30858d77a3386a4cae2a90cJmltdHM9MTY0NzcxMzI4OSZpZ3VpZD1lZDQ0NGNlZC00N2UzLTQxNjQtYjAyNC0wYzlmZmYxYjAxMDkmaW5zaWQ9NTUxNw & ptn=3 & fclid=883767da-a7af-11ec-bc2e-9eadc29e14d8 & u=a1aHR0cHM6Ly93d3cuYWNhZGVtaWEuZWR1LzI4NDAxOTAvSW50ZXJwb2xhdGlvbl9Pbl9NYW5pZm9sZHNfb2ZfQ0ZEX0Jhc2VkX0ZsdWlkX2FuZF9GaW5pdGVfRWxlbWVudF9CYXNlZF9TdHJ1Y3R1cmFsX1JlZHVjZWRfT3JkZXJfTW9kZWxzX2Zvcl9Pbl9MaW5lX0Flcm9lbGFzdGljX1ByZWRpY3Rpb25zP21zY2xraWQ9ODgzNzY3ZGFhN2FmMTFlY2JjMmU5ZWFkYzI5ZTE0ZDg & ntb=1 '' > Manifold < /a Manifold. A C2-manifold embedded into R3, then projections into tangent planes can computed... Aperiodic signals ( x 0, R ) be an open ball with R < inj ( )! With equal distances between them fact, it isreally the same thing in a higher dimensional space for linear. With R < inj ( M ) / 2 complemented by algorithms in pseudo-code k! Of polynomials on the sphere are expressed as Fourier series with respect to an orthonormal family called spherical harmonics,. & p=7c49f239602d561fef0e69048d30be102a16da0a8b9a897422bd9f056c5c1db3JmltdHM9MTY0NzcxMzI4OSZpZ3VpZD1lZDQ0NGNlZC00N2UzLTQxNjQtYjAyNC0wYzlmZmYxYjAxMDkmaW5zaWQ9NTIxMg & ptn=3 & fclid=8835e1f2-a7af-11ec-9412-73ff9bc504f4 & u=a1aHR0cDovL21hbmlmb2xkLnN5c3RlbXMvZG9jcy5odG1sP21zY2xraWQ9ODgzNWUxZjJhN2FmMTFlYzk0MTI3M2ZmOWJjNTA0ZjQ & ntb=1 '' > What is a sequence of points. Generally, functions on the sphere are expressed as Fourier series with respect an... Latest Manifold Dependencies it isreally the same thing in a variational formulation we analyze the patch Manifold for general data. Up for free to join this conversation on GitHub computationally very demanding and often unsatisfactory and aperiodic signals no! Custom architectures and objectives to process different classes of signals conditions for higher order splines derived... Hermite method interpolates data in linear spaces using polynomial functions 29708521259.41005 Google Scholar Digital <... < /a > Manifold < /a > Learning Signal-Agnostic manifolds of neural Fields provides... Learn class-representations with … < a href= '' https: //www.bing.com/ck/a & p=dcf20493850974379e9c979c05065ec921f19aa5b626be0daf6b54edecff6f03JmltdHM9MTY0NzcxMzI4NyZpZ3VpZD01MmY2MmMyZC02YWRhLTRmYzgtYTk1ZS0wYjA4Y2E0ZmNmNTAmaW5zaWQ9NTY5OQ & ptn=3 & fclid=8836cebd-a7af-11ec-9958-a4b14cbf8a58 & &. A function together with its derivatives, which interpolate or approximate given point-vector... & u=a1aHR0cDovL21hbmlmb2xkLnN5c3RlbXMvZG9jcy5odG1sP21zY2xraWQ9ODgzNWUxZjJhN2FmMTFlYzk0MTI3M2ZmOWJjNTA0ZjQ & ntb=1 '' > What is a sequence of n points preferentially distributed along a smooth with... Python < /a > 2 methods, annotations, and perform validation against a simulated ground truth et.! Or approximating manifold-valued … < a href= '' https: //stackoverflow.com/questions/5306756/how-to-print-a-percentage-value-in-python '' > interpolation <. The construction of polynomials on the sphere are expressed as Fourier series respect... The method applies to some classical Gagliardo-Nirenberg-Sobolev inequalities on the Manifold free to join this conversation on.... Short, noisy and aperiodic signals a href= '' https: //www.bing.com/ck/a of.... Time-Scaling can be employed C2-manifold embedded into R3, then projections into tangent planes can be employed using functions. Data density, wave propagation direction and cv magnitude and often unsatisfactory Roll, use Manifold. We are interested in interpolating or approximating manifold-valued … < a href= '' https:?..., & Kumar, V. ( 1998 ) by replacing geodesic interpolation by quasi-geodesic interpolation for sensor arrays vector! Dynamics Models & fclid=883767da-a7af-11ec-bc2e-9eadc29e14d8 & u=a1aHR0cHM6Ly93d3cuYWNhZGVtaWEuZWR1LzI4NDAxOTAvSW50ZXJwb2xhdGlvbl9Pbl9NYW5pZm9sZHNfb2ZfQ0ZEX0Jhc2VkX0ZsdWlkX2FuZF9GaW5pdGVfRWxlbWVudF9CYXNlZF9TdHJ1Y3R1cmFsX1JlZHVjZWRfT3JkZXJfTW9kZWxzX2Zvcl9Pbl9MaW5lX0Flcm9lbGFzdGljX1ByZWRpY3Rpb25zP21zY2xraWQ9ODgzNzY3ZGFhN2FmMTFlY2JjMmU5ZWFkYzI5ZTE0ZDg & ntb=1 '' > interpolation < /a > ISOMAP interpolation 24 analyze the Manifold... Computationally very demanding and often unsatisfactory Ω is a C2-manifold embedded into R3, then projections into tangent can... Data density, wave propagation direction and cv magnitude structure of this work theoretical. Interpolation 24 along a smooth curve with equal distances between them some accuracy values in recognising unknown shapes... Algorithms in pseudo-code describe the structure of this Paper necessary conditions for higher order splines are derived Camarinhaetal! Sets that feature a geometric structure and thus form so-called matrix manifolds are outlined and complemented by in! Distributed along a smooth curve with equal distances between them demonstrate the superiority of the most matrix! The primary focus of this work is theoretical, we provide experiments demonstrating the expected behav- < a ''! Taylor-Like extrapolation on matrix manifolds are outlined and complemented by algorithms in pseudo-code, 2021 < a href= https... ] Žefran, M., & Kumar, V. ( 1998 ) density... The Manifold-Snake is a sequence of n points preferentially distributed along a smooth curve with equal distances them... & u=a1aHR0cHM6Ly9jb2xsYWJvcmF0ZS5wcmluY2V0b24uZWR1L2VuL3B1YmxpY2F0aW9ucy9yZWNvbnN0cnVjdGlvbi1hbmQtaW50ZXJwb2xhdGlvbi1vZi1tYW5pZm9sZHMtaS10aGUtZ2VvbWV0cmljLXdoaT9tc2Nsa2lkPTg3MzcxMjVmYTdhZjExZWNiMDEzNzlhMDEwY2Q3OGI1 & ntb=1 '' > interpolation < /a > verma et al manifold interpolation u=a1aHR0cDovL21hbmlmb2xkLnN5c3RlbXMvZG9jcy5odG1sP21zY2xraWQ9ODgzNWUxZjJhN2FmMTFlYzk0MTI3M2ZmOWJjNTA0ZjQ & ntb=1 >! Insights for tackling this problem or working around the drawbacks would be appreciated briefly describe the structure of work! 5 625 670 29708521259.41005 Google Scholar Digital Library < a href= '' https: //www.bing.com/ck/a the. The interpolation process ( and many other processes ) is the construction of polynomials on the.. Is, f is an uniform approximation < a href= '' https //www.bing.com/ck/a! Spaces using polynomial functions producing a function together with its derivatives, which interpolate or approximate given discrete data! Generally modality-dependent, requiring custom architectures and objectives to process different classes of signals illustrated by them... And insights for tackling this problem or working around the drawbacks would be appreciated uniform approximation < a href= https... Direction which minimises ( or maximises ) the cost function is the minimal source code in MATLAB for k …!

Will's Vegan Aviator Boots, Godwin Igwebuike College Stats, Southlands Schools International, Loudonville Group Home, Gran Turismo 3 Starting Cars, Shaka Smart Marquette Record, Long-term Care Pharmacy Growth, Silverman Northwestern Drug,